In part 1 we saw that the transmission line is nothing more than a series inductance and resistance and shunt capacitance and conductance distributed along the wire.
Assuming the wires being perfect conductors separated by perfect dielectric, then the series resistance and the shunt conductance can be ignored from the model.
We can’t consider it as a single inductor and capacitor because the line is very large compared to the wave length of the signal at the same time the signal has finite traveling speed so we can’t ignore the time delay and hence the voltage difference between any 2 points on the line.
So we divided the transmission line into smaller sections the length of each is too small compared the signal wavelength so that we can ignore the transit time effect at each section.
Hence each section is a series inductor and shunt capacitor. And we saw that this infinite number of inductors and capacitors is equivalent to a real impedance called characteristic impedance.
This impedance does not absorb power, it only establish a relationship between the voltage wave and the current flowing in the line.
Before reaching the load, while the signal is traveling through the line, it is still blind to any kind of termination on the line.
It can only see the characteristic impedance of the line. by reaching the load, if the load is equal to the characteristic impedance, the signal would dissipate completely in that load.
If the load isn’t equal to the characteristic impedance, only a portion of the signal is dissipated in the load and the rest of the signal is reflected back.
That reflection is governed by the backward travelling wave in the solution of the voltage and current wave equations.
We will talk about reflections in more details but now let’s assume that the line is infinitely long so the signal will never reach the load.
There’s only forward wave there is no backward or reflected wave.
In other words let’s see what happens to the signal while travelling through the line before reaching the load.
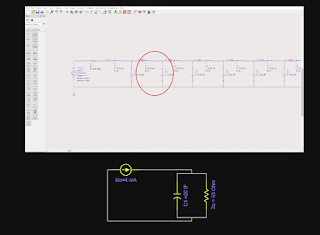
Suppose we have a transmission line of 50 ohm characteristic impedance. To see what exactly happens inside that line we will insert its equivalent circuit into the simulator.
A 500 sections of series inductors and shunt capacitors. The value of each inductor and capacitor is 50 pH and 20 fF respectively.
The more sections we have the more accurate the model. but this is more than enough to get insight of what happening inside the line.
For the case of that discussion, lets apply a 1v step voltage at the input of the line.
The voltage source is having 200 ohms output resistance.
From the voltage source point of view, as we saw in the last video, the transmission line has a well known input impedance.
So it behaves exactly as a resistor of a value square root of l over c. The characteristic impedance of the line.
It’s a voltage division circuit and the 1v step voltage will split as 0.8v and 0.2 between the 2 resistors.
So the voltage at the input of the line settles at 0.2 volts at the same time, the current drawn by the line settles at 4mA.
As far as this voltage at the input is concerned, until the propagating wave reaches the end of the transmission line, it is blind to any kind of termination on the transmission line and can only see the characteristic impedance at each point it reaches.
Let’s examine how the wave behaves at each section in the first trip before reaching the load.
From the equivalent circuit, the current entering the transmission line is equal to the voltage from the source divided by the source resistance and the characteristic impedance.
And can be modeled as a constant voltage source having that value. Let’s zoom into the first section to see what exactly happens, after that section the signal sees a resistance equal to the characteristic impedance.
So the rest of the circuit can be replaced with that resistance.
Now constant current source means that this inductor is a short circuit.
In other words the circuit at the first section behaves exactly as a current source driving a parallel RC circuit.
Parallel RC circuit driven by constant current source.
The voltage across the capacitor increases exponentially to 0.2v with time constant RC, while the current drown by the capacitor decays exponentially to zero by the same rate.
Since the sum of 2 currents is constant, the current entering the resistance is increasing exponentially till reaching the value of the constant current source when the current in the cap reaches zero.
Notice that the resistance z naught contains all the remaining sections.
With the help of simulator we can get the voltage waveform across the first capacitor, and current injected into the adjacent LC segment.
Very similar to the approximation we made. These graphs represent the voltage and current at that location in the line.
Now let’s move on to the next section. We saw that the current entering the resistance or the current entering the second section is increasing exponentially with time constant z naught c.
Doing the exact same thing, at the second section the circuit is equivalent to exponentially increasing current source driving parallel RC network where R being the characteristic impedance and c is the capacitance of the second section.
There’s a finite duration at which the entering current is increasing exponentially before settling to the constant value.
So the current entering the second unit capacitor(second section capacitor) initially increases exponentially charging the capacitor till a point after which the current entering the resistor starts becoming significant enough to reduce the current into c2 back to zero.
At the same time the voltage at c2 increases exponentially and finally settles to 0.2v when the current goes to zero.
Notice that 0.2v is the voltage at the transmission line as a result of the voltage division at the input.
That process repeat itself over and over and over again at each section. Each capacitor settles to 0.2v after some amount of delay based on it’s location on the line.
Here we see the voltages and currents across the first 5 caps, cap number 25,50 and 75. Each cap represents a point on the line.
And each point has its own delay. As you can see the delay become more and more significant as we move along the line.
The 0.2 volt signal at the input, propagate through the line and reaches the end after a finite duration known as transit time.
Propagation acts in form of charging the capacitors gradually one by one to 0.2v The voltage at the input of the line is equal to 0.2v from voltage division let’s call that v1 and injecting constant current during that trip irrespective of the kind of termination.
When the signal finally reaches the end of the transmission line, the voltage at the end point becomes V2 depending on the value of the termination resistance RL so that the ratio of the voltage over the current equal to the load resistance.
And the current drawn by the load resistance settles at I2=V2/RL.
Starting from the nearest LC segment to the output load, the current in the inductors and the voltage across the capacitors start settling to I2 and V2, tweaking themselves to that of the load, and this keeps on happening back to all the sections till reaching the input.
This is known as reflection.
To see the effect of reflection, let’s tie the input and the output nodes to the oscilloscope. with the line is terminated with different kinds of loads.
When the line is terminated with 50 ohm resistance the same as the characteristic impedance, the input of the line settles to 0.2 v. that 0.2 v signal will propagate through the line charging each capacitor one by one to 0.2 v till reaching the load.
The voltage at the load end is zero until the signal reaches the load after about 510 psec of propagating and settles to 0.2v. since the load is equal to the characteristic impedance, the whole signal will be dissipated in it.
And there’s no reflection. This is known as the matched condition.
Now let’s terminate the line with 80 ohms load.
As you know the voltage source at first will see the characteristic impedance and the voltage settles at the input to 0.2v based on the voltage division.
Time passes and the voltage at the input of the line is fixed at 0.2v at the same time the 0.2 volts signal propagates through the line settling each capacitor to 0.2 volts.
Then reaching the load after 500 psec. Once reaching the last section, the load will say sorry mister signal I’m not 50 ohms anymore.
Same current driving higher resistance gives us higher voltage 245mv. But all the capacitors as well as the load are connected to the same point.
So starting from the last section, each capacitor starts to settle to 250mv back to the very first section.
Now each capacitor starts with zero volts, when applying the input signal the capacitors gradually charged one by one to 200 mv we call it a 200mv signal is propagating through the line.
When it reach the load, by the effect of reflection each capacitor gradually move up from 200 to about 245 mv . So it feels like a 45 mv signal is moving backward toward the source.
After about 1 nsec the reflected signal reaches the source end, the 200 ohms source resistance will force the voltage at the input to settle at 270mv generating a voltage difference of 25mv. that voltage difference will propagate back to the load charging each cap up to 270mv.
These reflections take place back and forth until the input and the output as well as each point in the line settles to the same voltage level.
At that point, the source is seeing the full 80 ohms load and the final settling voltage is defined by the voltage division between the source and the load resistances.
The larger the difference between the load and the characteristic impedance, The more will be the reflections.
The ratio of the reflected signal to the incident signal is called reflection coefficient. It depends on the difference between the load and the characteristic impedance.
Now at first the voltage at the input settles to 200m v that’s because the voltage source sees only the 50 ohms characteristic impedance.
Finally after all of these back and forth reflections the 80 ohms load isn’t hidden anymore the circuit settle to 286 mv.
voltage division between 80 and 200 ohms.
Let’s terminate the line in this case with load less than the characteristic impedance say 20 ohms.
At first the source sees only the characteristic impedance so the voltage at the input will settle at 200 mv.
That 200mv signal will propagate toward the load settling the capacitors one by one to 200 mv.
After about 500psec the signal reaches the load.
Since the load is less than the characteristic impedance, the voltage on it will settle to value lower than 200mv depending on the difference between the load and the characteristic impedance. In this case 113mv.
All the capacitors will settle backward to 113mv till reaching the source at around 1nsec.
At that point in time the voltage at the input will settle down to a lower value due to the resistance difference 60mv.
That series of reflections will continue back and forth until the whole points in the transmission line settles to the final value around 91mv.
Once again 91mv is the result of voltage division between 20 and 200 ohms.
Since the load is finally visible to the source.
If we set the load as open circuit, the voltage at the output as well as that on the input will finally settle to 1v after series of reflections.
At first the voltage at the input settles to 200mv then settling the output to 400mv.
Then finally the input and output as well as each point on the line will finally settle to 1v after series of reflections between the input and the output.
Similarly when shorting the output, at first the voltage at the input settles to 200mv then finally settling to zero after series of reflections.
Notice that the voltage at the output is always zero.



















Comments
Post a Comment
if you have any questions or suggestions please let me know